2025年07月27日
目次
お金の時間価値とは?
MBAの受験にはファイナンスの基礎でもあるお金の時間価値・単利・複利の概念を理解しておく必要があります。これらの詳細はそれぞれ次の通りです。
1-1.お金の時間価値

お金の時間価値とは「現在と将来のお金の価値が異なる事」を言います。基本的にお金とは同額でも現在と将来とでは価値が異なります。その理由は次の三つです。
1.投資で増やすことができる。
まず一点目は「投資で増やすことができる」という点になります。例えばあなたが現在100万円を有しているとします。今この瞬間にこの100万円を特定の株式や債券に投資をすれば、1年後はそれ以上の金額になっている可能性があります。株式の場合は不確実性が高いものになりますが、財政が健全な国家の国債などを購入すればほぼ確実に利回りを獲得する事ができます。このように現在のお金は投資で増やす事ができます。
2.インフレで価値が落ちる。
次に二点目は「インフレで価値が落ちる。」という点になります。上記の例と同じくあなたが現在100万円を有しているとします。この100万円を現金で保管している場合、インフレにより価値が減少する事になります。例えばインフレ率(物価上昇率)が3%であると仮定すると、あなたの持つ100万円の価値は1年後に約3%下落する事になります。(正確には「100/1.03=約97.09万円程度」になります。)このように現在のお金の価値と将来のお金の価値は異なるものになります。ただしデフレ下ではこの逆になりお金の価値は上昇する事になります。
3.不確実性がある。
三点目は「不確実性がある。」という点になります。例えばあなたが「今すぐ100万円受け取るか1年後に100万円を受け取るか決めなさい。」と言われたら、今すぐ100万円を受け取る方を選択すると思います。これは上記の投資やインフレ率を考慮すると当然ですよね。ただし「この100万円は投資する事ができずインフレ率は0%と仮定する。」と言われても、やはり今すぐ100万円を受け取る方を選択すると思います。何故なら1年後にそのお金を本当に受け取れるかどうか不明だからです。この100万円をくれるのが民間企業や個人ならもちろんですが、たとえ国家から言われたとしても、国家も破綻する可能性がありますよね。もしくは何らかの理由で約束が反故にされる可能性も完全には否定できません。よって今すぐお金を受け取る方が価値が高いと言えます。
利息のしくみ:単利
利息には「単利と複利」があります。その詳細はそれぞれ次の通りになります。
2-1.単利とは?
まず「単利とは元金に対してのみ利息が計算される仕組み」になります。具体的な例を挙げると次の通りです。
「単利で利息10%と仮定」
| 年 | 現金 | 増加額 |
| 現在 | 100万円 | 0円 |
| 1年後 | 110万円(+100万円×10%) | 10万円 |
| 2年後 | 120万円(+100万円×10%) | 10万円 |
| 3年後 | 130万円(+100万円×10%) | 10万円 |
| 4年後 | 140万円(+100万円×10%) | 10万円 |
| 5年後 | 150万円(+100万円×10%) | 10万円 |
上記の通り単利では最初の元金を基に利息が計算されます。追加された利息は元金には組み込まれません。現在のお金が100万円で利息が10%なら上記の通り毎年10万円ずつ増え続けていきます。これが単利の仕組みになります。
2-2.単利の計算式

単利で増加する金額は「現在価値×(1+r×n)」という式で計算する事ができます。 (r=利率・n=年数)
この公式により単利のN年後の金額を簡単に計算する事ができます。例を挙げます。例えばあなたが400万円の現金を有しており、単利で年間3%の利息が発生するとします。この条件であなたが3年間預金を運用した場合、3年後にあなたの400万円は「400万円×(1+0.03×3)」=436万円になっています。この内400万円は元金で36万円(年間12万円×3年分)が利息になります。別の例を挙げます。例えばあなたが600万円を有しており、金利が5%で5年間運用すると、この600万円は「600万円×(1+0.05×5)」=750万円になります。この内600万円が元金で150万円(年間25万円×5年分)が利息になります。これが単利の計算方法になります。基本的に現代の金融の実務では単利は採用されていません。
利息のしくみ:複利
3-1.複利とは?
まず「複利とは毎年利息が元金に取り入れられる仕組み」になります。複利の具体的な例を挙げると次の通りです。
「複利で利息10%と仮定」
| 年 | 現金 | 増加額 |
| 現在 | 100万円 | 0円 |
| 1年後 | 110万円(+100万円×10%) | 10万円 |
| 2年後 | 121万円(+110万円×10%) | 11万円 |
| 3年後 | 133.1万円(+121万円×10%) | 12.1万円 |
| 4年後 | 146.41万円(+133.1万円×10%) | 13.31万円 |
| 5年後 | 161.051万円(+146.41万円×10%) | 14.641万円 |
上記の通り複利では毎年利息が元金に組み込まれていきます。現在のお金が100万円で利息が10%なら1年後は10万円の利息が発生しますが、2年後はその110万円を基に10%の利息が計算されます。以降、同じ計算が続いていきます。
3-2.複利の計算式

複利で増加する金額は「現在価値×(1+r)ⁿ」という式で計算する事ができます。(r=利率・n=年数)
この計算式により複利のN年後の金額を簡単に計算する事ができます。例を挙げます。例えばあなたが300万円の現金を有しており、複利で年間2%の利息が発生するとします。この条件であなたが5年間預金を運用した場合、5年後にあなたの300万円は「300万円×(1+0.02)⁵」=約331万円になっています。この内300万円は元金で約31万円が利息になります。別の例を挙げます。例えばあなたが500万円を有しており、金利が5%で5年間運用すると、この500万円は「(1+0.05)⁵」=約638万円になります。仮に500万円を5年間5%という条件で単利で運用すると625万円になります。つまり約638万円ー625万円=約13万円が複利によって増加したと言えます。これを「複利効果」と言います。基本的に現代の金融の実務では複利が採用されています。
単利と複利の特徴
4-1.単利の特徴
単利の特徴は「管理・計算がしやすいので短期の投資に向いている」という点になります。
例えばあなたが1年以内にお金を貸し借りする場合や1年以内の短期投資を行う場合は単利しか使用しません。また1年以上でも比較的短期間の場合は複利と比べて大きな差は生まれないので、単利の「利息の管理がしやすい」というメリットが生きてきます。しかし複利と比べると、資産を増加させるという観点からは単利より複利の方が適していると言えます。
4-2.複利の特徴
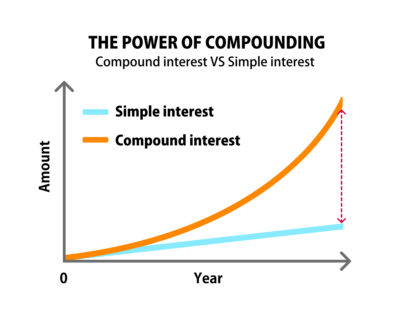
複利のメリットは「利息が利息を生むことで資産が時間とともに加速度的に増加する点」という点になります。
上記の通り複利には「複利効果」があります。複利と単利を比較すると資産の増加率の変化は右のグラフようになります。そのため資産を増加させたい場合は複利の方に軍配が上がるのは論を俟たないと言えます。しかし複利の場合は計算が複雑であるというデメリットがあります。仮に計算機やコンピューターを使用しても、場合によっては人間の確認が必要になるので、その分だけ手間が掛かると言う事ができます。そのため金額が大きい場合は別ですが、金額が小さい場合は複利だと手間に掛かるコストの方が高くなってしまう可能性があります。これが複利のデメリットになります。
ファイナンスの基礎
以上がファイナンスの基礎になります。上記はこれからファイナンスを学んでいくMBA受験生であるあなたにとって非常に重要な内容になりますので、しっかりと理解して覚えておくようにしましょう。そしてファイナンスの観点から企業の財務を分析できるようになりましょう。